MECÂNCIA GENERALIZADA GRACELI DE INTERAÇÕES E TRANSFORMAÇÕES.

LEI -

TODA INTERAÇÃO LEVA A TRANSFORMAÇÕES, E VICE-VERSA.

INTERAÇÕES COMO E EM:

NAS INTERAÇÕES DAS FORÇAS FUNDAMENTIAS.

INTERAÇÕES DE SPIN - ÓRBITA.

ESTRUTURA - TEMPERATURA.

DISTRIBUIÇÃO ELETRÔNICA - NÍVEIS DE ENERGIA - BANDAS.

ELÉTRONS - FÓNOS.

ELÉTRONS - ELÉTRONS.

ESTADO QUÂNTICO - NÚMERO QUÃNTICO.

ENTROPIA -TEMPERATURA - MOVIMENTO BROWNIANO - CAMINHOS DE PARTÍCIULAS.

CATEGORIA - DIMENSÕES - FENÔMENOS [NO SISTEMA SDCTIE GRACELI].

ENTROPIA - ENTALPIA. ETC.

VEJAMOS AS INTERAÇÕES DE CAMPOS.

E EM RELAÇÃO AO SISTEMA DE MECÂNICA GENERALIZADO GRACELI.

eletromagnetismo quântico químico relativístico Graceli.

MECÂNICA DO SISTEMA DIMENSIONAL GRACELI.

ONDE A MAIORIA DOS FENÔMENOS FÍSICOS [EM TODAS AS ÁREAS] VARIAM CONFORME O SISTEMA DIMENSIONAL GRACELI.

SENDO ELE;

EQUAÇÃO GERAL DE GRACELI.[quantização de Graceli].

G ψ = E ψ = IGFF $\psi ^{*}$ E [tG+].... .. =

G ψ = E ψ = IGFF $\psi ^{*}$ E [tG+] $\lambda$ ψ ω ${\mathcal {T}}$ /c] = $\,N_{A}$ $\,M$ $\,z^{+}$ $\,z^{-}$ $\,e$ [/ $\,\epsilon _{o}$ ] / $\,r_{0}$ / = $\lambda$ ħω $q\ \$ [Ϡ ] [ξ ] [,ς] $g_{s}$ $\epsilon _{s}$ [ $\epsilon _{s}$ q G*] ${\begin{pmatrix}\psi _{0}\\\psi _{1}\end{pmatrix}}$ ψ μ / h/c ψ(x, t) $-i\hbar {\frac {\partial }{\partial x_{n}}}$ x t ]..

[ $\epsilon _{s}$ q [tG*] ==G ψ = E ψ = IGFF $\psi ^{*}$ E [tG+].... ..

SISTEMA GRACELI DE:

TENSOR [tG+] GRACELI = IGFF + SDCTIE GRACELI, DENSIDADE DE CARGA E DISTRIBUIÇÃO ELETRÔNICA, NÍVEIS DE ENERGIA, NÚMERO E ESTADO QUÂNTICO. + POTENCIAL DE SALTO QUÂNTICO RELATIVO AOS ELEMENTOS QUÍMICO COM O SEU RESPECTIVO E ESPECÍFICO NÍVEL DE ENERGIA., POTENCIAL DE ENERGIA, POTENCIAL QUÍMICO, SISTEMA GRACELI DO INFINITO DIMENSIONAL.

ONDE A CONFIGURAÇÃO ELETRÔNICA TAMBÉM PASSA A SER DIMENSÕES FÍSICO-QUÍMICA DE GRACELI.

[ $\epsilon _{s}$ q [tG*] = energia quântica Graceli.

Força fundamental - INTERAÇÕES GRACELI IG =

IGFF = INTERAÇÕES GRACELI - Força fundamental.

T = TEMPERATURA.

PERMEABILIDADE MAGNÉTICA .

INTERAÇÃO SPINS ÓRBITA.

MOMENTUM MAGNÉTICO.

DISTRIBUIÇÃO ELETRÔNICA DOS ELEMENTOS QUÍMICOS.

NÍVEIS E SUBNIVEIS DE ENEREGIA.

BANDAS DE ENERGIAS.

IGFF = FF / T . PM. ISO . MM. DEEQ. NE. BE. [1]

IGFF = FF / T . PM. ISO . MM. DEEQ. NE. BE./G ψ = E ψ =

\psi ^{*}

E [tG+].... .. [2]

1 / IGFF = FF / T . PM. ISO . MM. DEEQ. NE. BE. [-1]

1 / IGFF = FF / T . PM. ISO . MM. DEEQ. NE. BE./G ψ = E ψ =

\psi ^{*}

E [tG+].... .. [-1]

RELATIVIDADE DAS FORÇAS FUNDAMENTAIS.

IGFF = FF / T . PM. ISO . MM. DEEQ. NE. BE. / c .

IGFF = FF / T . PM. ISO . MM. DEEQ. NE. BE./G ψ = E ψ =

\psi ^{*}

E [tG+].... ../ c .

Piroeletricidade (do grego pyr, fogo, e eletricidade) é a capacidade de alguns materiais de gerarem temporariamente um potencial elétrico quando aquecidos ou arrefecidos. A mudança de temperatura modifica ligeiramente as posições dos átomos na estrutura cristalina, de tal modo que a polarização do material é alterada. Esta alteração da polarização dá origem a um potencial elétrico temporário, que desaparece após o tempo de relaxação dielétrica.^[1]

A piroeletricidade não deve ser confundida com termoeletricidade, onde um perfil térmico fixo, não-uniforme, dá origem a uma diferença de potencial elétrico permanente.

Explicação

A piroelericidade pode ser visualizada como um dos lados de um triângulo, no qual cada vértice representa estados de energia do cristal: energia cinética, elétrica e térmica. O lado entre os vértices elétrico e térmico representa o efeito piroelétrico e não produz energia cinética. O lado entre os vértices cinético e elétrico representa o efeito piezoelétrico e não produz calor.

Embora tenham sido concebidos materiais piroelétricos artificiais, este efeito foi inicialmente descoberto em minerais como a turmalina. O efeito piroelétrico está também presente nos ossos e tendões.

A carga piroelétrica nos minerais desenvolve-se nas faces opostas de cristais assimétricos. A direção para a qual tende a propagação da carga é usualmente constante ao longo do material piroelétrico, mas em alguns materiais esta direção pode ser alterada por um campo elétrico próximo. Estes materiais dizem-se ferroelétricos. Todos os materiais piroelétricos são também piezoelétricos. Note-se contudo, que alguns materiais piezoelétricos têm uma simetria cristalina que não permite a piroeletricidade.

História

A primeira referência ao efeito piroelétrico encontra-se nos escritos de Teofrasto em 314 a.C., que notou que a turmalina atraía palhas e cinzas quando aquecida. As propriedades da turmalina foram redescobertas em 1707 por Johann Georg Schmidt, que reparou nas propriedades atrativas do mineral quando aquecido. A piroeletricidade foi descrita pela primeira vez - apesar de não ter sido assim designada - por Louis Lemery em 1717. Em 1747 Lineu associou pela primeira vez o fenómeno à eletricidade, o que só veio a ser demonstrado por Franz Ulrich Theodor Aepinus, em 1756.

O estudo da piroeletricidade tornou-se mais sofisticado no século XIX. Em 1824 David Brewster deu ao efeito o nome que hoje tem. Tanto William Thomson em 1878, como Woldemar Voigt em 1897, ajudaram a desenvolver uma teoria para os processos por detrás da piroeletricidade. Pierre Curie e o seu irmão, Jacques Curie, estudaram a piroeletricidade na década de 1880, o que conduziu à descoberta de alguns dos mecanismos por detrás da piezoeletricidade.

Classes cristalinas piroelétricas

As estruturas cristalinas podem ser divididas em 32 classes, ou grupos pontuais, segundo o número de eixos rotacionais e planos de reflexão que exibem e que mantém a estrutura do cristal piroelétrico. Entre as 32 classes de cristais, vinte e uma são não-centrossimétricas (não têm centro de simetria). Destas vinte e uma, vinte exibem piezoeletricidade direta, sendo a restante a classe cúbica 432. Dez destas vinte classes piezoelétricas são polares, i.e., exibem uma polarização espontânea, tendo um dipolo na sua célula unitária, e exibem piroeletricidade. Todos os cristais polares são piroelétricos.

Classes de cristal piezoelétricas: 1, 2, m, 222, mm2, 4, -4, 422, 4mm, -42m, 3, 32, 3m, 6, -6, 622, 6mm, -62m, 23, -43m

Piroelétricas: 1, 2, m, mm2, 3, 3m, 4, 4mm, 6, 6mm

Desenvolvimentos recentes

Têm sido feitos progressos na criação de materiais piroelétricos artificiais, usualmente na forma de uma película fina, a partir de nitreto de gálio (Ga N), nitrato de césio (Cs N O₃), fluoretos de polivinila, derivados de fenilpirazina, e ftalocianina de cobalto (ver cristal piroelétrico). O tantalato de lítio (Li Ta O₃) é um cristal que exibe tanto propriedades piezoelétricas como piroelétricas que tem sido usado para criar fusão nuclear em pequena escala ("fusão piroelétrica").^[2]

Descrição matemática

O coeficiente piroelétrico pode ser descrito como a variação do vetor de polarização espontânea com a temperatura^[3]:

p_{i}={\frac {\partial P_{S,i}}{\partial T}}

/ G ψ = E ψ =

\psi ^{*}

E [tG+].... ../ c

em que p_i (Cm^-2K^-1) é o vetor do coeficiente piroelétrico.

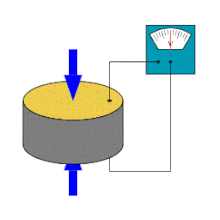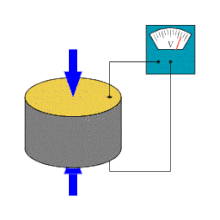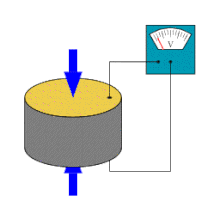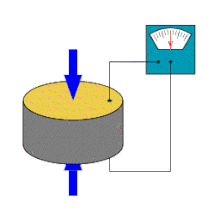
Piezoeletricidade é a capacidade de alguns cristais gerarem tensão elétrica por resposta a uma pressão mecânica. O termo piezoeletricidade provém do grego piezein, que significa apertar/pressionar. Referente à geração de corrente elétrica, juntou-se a designação eletricidade, de modo que piezoeletricidade é interpretado como a produção de energia elétrica devido à compressão sobre determinados materiais.

Mecanismo

Um disco piezoelétrico gera uma diferença de potencial quando deformado.

O efeito piezoelétrico é entendido como a interação eletromecânica linear entre a força mecânica e o estado elétrico (forças de Coulomb) em materiais cristalinos (cerâmicos, polímeros).

O efeito piezoelétrico é um processo reversível em que os materiais exibem o efeito piezoelétrico direto (a geração interna de carga elétrica resultante de uma força mecânica aplicada), mas também exibem o efeito piezoelétrico reverso (a geração interna de uma tensão mecânica resultante de um campo elétrico aplicado). Por exemplo, os cristais de titanato zirconato de chumbo irão gerar piezoeletricidade mensurável quando a sua estrutura estática é deformada por cerca de 0,1% da dimensão inicial. Por outro lado, esses mesmos cristais mudam cerca de 0,1% da sua dimensão estática quando um campo elétrico externo é aplicado ao material. Como exemplo, o efeito piezoelétrico inverso é usado na produção de ondas de ultrassom.^[1]

Cristais

Utilizando argumentos referentes à simetria, o efeito piezoelétrico não existe em materiais que apresentam simetria central, e desta forma, podem ser polarizados, ou seja, a piezoeletricidade pode ser explicada pela assimetria de polarização iônica. Porém, elementos puros, tais como selênio (Se) e telúrio (Te) também exibem a propriedade de piezoeletricidade. Nestes casos, a polarização elétrica induzida é atribuída à distribuição eletrônica, que é alterada pela ação externa.

Considerando as trinta e duas classes de cristais catalogadas, 21 não são centrossimétricas (não possuem centro de simetria); vinte destes exibem piezoeletricidade direta; dez destes representam as classes de cristal polares, que mostram uma polarização espontânea, sem estresse mecânico devido a um momento de dipolo elétrico permanente. Se o momento de dipolo puder ser revertido por meio da aplicação de um campo elétrico externo, então o material é considerado ferroelétrico.

Para cristais polares, para os quais o momento de dipolo P diferente de zero se mantém sem se aplicar uma carga mecânica, o efeito piezoelétrico manifesta-se alterando a magnitude ou a direção do vetor momento de dipolo ou ambos. Para os cristais não-polares, mas piezoelétricos, a polarização diferente de zero é apenas induzida pela aplicação de uma carga mecânica. Para eles, a tensão pode ser imaginada para transformar o material a partir de uma classe de cristal não polar (P = 0) para uma polar, para a qual P ≠ 0.

A maioria dos cristais não possui propriedades piezoelétricas. O mais importante cristal natural que possui esta propriedade é o quartzo. Além deste, pela facilidade de sintetização, os cristais utilizados são cerâmicas à base de, por exemplo, titanato de bário ou zirconato de chumbo.^[2]

Descrição matemática

A piezoelectricidade é uma combinação de efeitos do comportamento elétrico do material:^[3]

D=\varepsilon E+eS\;

Nessa equação, D é o deslocamento elétrico, ε é a permissividade elétrica, E representa o campo elétrico, 'e' representa a constante de stress e S é a tensão longitudinal aplicada.

Quando a aplicação de uma força F, o centro de equilíbrio das cargas positivas e negativas é deslocado, causando a polarização do material, e o consequente deslocamento de corrente.

Similarmente, considerações para o caso quando um campo elétrico E é aplicado mostram que um termo referente a stress adicional, -eE, aparece. Tem-se então a Lei de Hooke, T = cS:

T=cS-eE\;

Se as cargas de moléculas positivas e negativas possuem magnitudes diferentes, há uma polarização espontânea. Se uma molécula possui um momento de dipolo, este material exibe uma polarização iônica. Já no caso onde há somente um tipo de elemento, mas este é polarizável, temos o efeito de polarização eletrônica.

A piezoeletricidade apresenta relação entre propriedades elétricas (E, D) e mecânicas (S, T). O modelo de um sólido piezoelétrico apresenta quatro diferentes relações entre variáveis. Assumimos que $T=T(S,E)$ e $D=D(S,E)$ . Assim, temos

dT=\left({\frac {\partial T}{\partial S}}\right)dS+\left({\frac {\partial T}{\partial E}}\right)dE

dD=\left({\frac {\partial D}{\partial S}}\right)dS+\left({\frac {\partial D}{\partial E}}\right)dE

onde todos os outros efeitos, tais como magnéticos e térmicos, assim como termos não-lineares, são ignorados.

Considerando o caso onde ao campo elétrico é aplicado sobre o material piezoelétrico (ao se colocar um material piezoelétrico num campo elétrico externo, as cargas elétricas da rede cristalina interagem com o mesmo e produzem tensões mecânicas), os segundos termos das equações acima enunciam o stress ou a tensão elétrica no material. Se o material não está confinado mecanicamente, a tensão será uma força de reação a força imposta pelo stress. Desta forma, a tensão altera a relação D e E, e assim a medição das propriedades elétricas dependentes das propriedades mecânicas. Do mesmo modo, uma tensão elétrica alterará a medição de propriedades mecânicas dependentes das propriedades elétricas. Em ambos os casos, isso demonstra a essência do acoplamento piezoelétrico. Para uma análise mais detalhada, deve-se comparar diferentes materiais piezoelétricos para identificar sua performance. Fatores como a eficiência do acoplamento a vibrações mecânicas, vibrações com campos elétricos externos, direção de aplicação do campo elétrico externo e demais, são resultados a serem considerados.

Num material piezoelétrico também interessam os seguintes coeficientes:

Coeficiente de acoplamento eletro-mecânico:

$K^{2}$ é definido como a variação de energia mecânica convertida em carga pela energia mecânica aplicada ao cristal, ou de modo similar, a energia elétrica convertida em energia mecânica pela energia elétrica aplicada ao cristal.

Coeficiente Dielétrica: esta grandeza relaciona a quantidade de carga que uma das faces do cristal pode armazenar em relação à carga total armazenada, e que pode ser dissipada como corrente real. Existem duas constantes dielétricas: uma é a constante para o cristal livre e outra para o cristal bloqueado:

$\varepsilon _{l}(1-K^{2})=\varepsilon _{b}$

Em física, termodinâmica, química, físico-química e física da matéria condensada, um ponto crítico, também chamado de estado crítico, ocorre sob condições (tais como valores específicos de temperatura, pressão ou composição) no qual não existem limites de fase. Existem vários tipos de pontos críticos, incluindo pontos críticos líquido-vapor e líquido-líquido.^[1]^[2]

Substâncias puras: ponto crítico líquido-vapor

O "ponto crítico" é por vezes usado para denotar o ponto especificamente vapor-líquido crítico de um material, a partir do qual a distinção entre fase a líquida e gasosa não existe.

O ponto crítico de vapor-líquido em um diagrama de fases pressão-temperatura está no extremo de alta temperatura do limite de fase líquido-gás. A linha pontilhada verde mostra o comportamento anômalo da água.^[3]

Como se mostra no diagrama de fases para a direita, isto é o ponto em que a fronteira entre a fase líquida e gasosa termina. Em água, o ponto crítico ocorre em cerca de 647 K. (374 ° C; 705 ° F) e 22,064 MPa (218 atm)

À medida que a substância se aproxima da temperatura crítica, as propriedades da sua fases gasosa e líquida convergem, resultando em apenas uma fase no ponto crítico: um fluido supercrítico homogêneo. O calor de vaporização é zero no ponto crítico e para além dele, por isso não existe distinção entre as duas fases. No diagrama de Pressão-temperatura, o ponto em que a temperatura crítica e pressão crítica satisfazer é chamado de ponto crítico da substância. Acima da temperatura crítica, um líquido não pode ser formada por um aumento da pressão, apesar de um sólido poder ser formado sob uma pressão suficiente. A pressão crítica é a pressão de vapor, à temperatura crítica. O volume crítico é o volume molar de uma mole do material a uma temperatura e pressão críticas.

Propriedades críticas variam de material para material, e para muitas substâncias puras estão prontamente disponíveis na literatura. No entanto, a obtenção de propriedades críticas para misturas é mais desafiador.

Definição matemática

No caso das substâncias puras, há um ponto de inflexão na curva isotérmica crítica (linha de temperatura constante) com um diagrama de Pressão-Volume. Isto significa que, no ponto crítico: ^[4]^[5]^[6]

\left({\frac {\partial p}{\partial V}}\right)_{T}=\left({\frac {\partial ^{2}p}{\partial V^{2}}}\right)_{T}=0

/ G ψ = E ψ =

\psi ^{*}

E [tG+].... ../ c

Isto é, as primeira e segunda derivadas parciais da pressão p no que diz respeito ao volume V são ambos zero, com as derivadas parciais avaliados em temperatura constante T. Esta relação pode ser usada para avaliar dois parâmetros de uma equação de estado em termos das propriedades críticas, tais como os parâmetros a e b na equação de van der Waals.^[4]

Às vezes um conjunto de propriedades reduzidas é definida em termos das propriedades importantes, isto é:^[7]

T_{r}=T/T_{c}\,

/ G ψ = E ψ =

\psi ^{*}

E [tG+].... ../ c

p_{r}=p/p_{c}\,

/ G ψ = E ψ =

\psi ^{*}

E [tG+].... ../ c

V_{r}={\frac {V}{RT_{c}/p_{c}}}\,

/ G ψ = E ψ =

\psi ^{*}

E [tG+].... ../ c

T_{c}=8a/27Rb,

/ G ψ = E ψ =

\psi ^{*}

E [tG+].... ../ c

V_{c}=3b\,

/ G ψ = E ψ =

\psi ^{*}

E [tG+].... ../ c

P_{c}=a/27b^{2},

/ G ψ = E ψ =

\psi ^{*}

E [tG+].... ../ c

onde $T_{r}$ é a temperatura reduzida, $p_{r}$ é a pressão reduzida, $V_{r}$ é a redução do volume, e $R$ é a constante universal dos gases.

O ponto de Draper é a temperatura aproximada acima da qual quase todos os materiais sólidos brilham visivelmente como resultado da radiação de corpo negro.^[1]^[2]^[3] Foi estabelecido em 525° C (798 K) por John William Draper em 1847.^[4]

Corpos a temperaturas logo abaixo do ponto Draper irradiam principalmente na faixa infravermelha e emitem luz visível insignificante. O valor do ponto de Draper pode ser calculado usando a lei de deslocamento de Wien: a freqüência $\nu _{\text{pico}}$ (em hertz) emitida por um corpo negro se relaciona com a temperatura da seguinte forma^[5]

\nu _{\text{pico}}=2.821{\frac {kT}{h}},

/ G ψ = E ψ =

\psi ^{*}

E [tG+].... ../ c

onde

k é Constante de Boltzmann,

h é Constante de Planck,

T é temperatura (em kelvins).

Substituir o ponto de Draper nesta equação produz uma freqüência de 83 THz, ou um comprimento de onda de 3,6 µm, que é bem dentro do infravermelho e completamente invisível ao olho humano. No entanto, a borda principal da curva de radiação do corpo negro se estende, em uma pequena fração do pico da intensidade, para o infravermelho próximo e vermelho-escuro (aproximadamente o intervalo 0,7-1 m), que são muito fracamente visíveis como um vermelho opaco.

De acordo com a lei de Stefan-Boltzmann, um corpo negro no ponto Draper emite 23 quilowatts de radiação por metro quadrado, quase exclusivamente infravermelho.

Células do ponto triplo

Células do ponto triplo são usadas na calibração de termômetros. Para medições exatas, células de ponto triplo são geralmente preenchidas com uma substância química com alta pureza, como o hidrogênio, argônio, mercúrio ou água, dependendo da temperatura desejada. A pureza destas substâncias pode ser tal que apenas uma parte em um milhão seja um contaminante, o que significa 99,9999% puro. As células de ponto triplo são tão eficientes no alcance de temperaturas precisas e reproduzíveis que um padrão internacional de calibração de termômetros chamado ITS-90 se baseia em células de hidrogênio, neon, oxigênio, argônio, mercúrio e água para determinar seus seis pontos definidos de temperatura.

Tabela de pontos triplos

Esta tabela lista o ponto triplo sólido-líquido-gasoso de substâncias comuns. A menos que diferentemente indicadas, as informações vieram da U.S. National Bureau of Standars (agora NIST (National Institute of Standards and Technology).^[6]

Substância	T [K]	p [kPa]*
Acetileno	192,4	120
Amoníaco	195,40	6,076
Argônio	83,81	68,9
Arsênio	1090	3628
Butano	134,6	7 × 10⁻⁴
Carbono (grafite)	4765	10132
Dióxido de carbono	216,55	517
Monóxido de carbono	68,10	15,37
Clorofórmio	175,43	0,870
Deuterio	18,63	17,1
Etano	89,89	8 × 10⁻⁴
Etanol	150	4,3 × 10⁻⁷
Etileno	104,0	0,12
Ácido fórmico	281,40	2,2
Hélio-4 (ponto lambda)	2,19	5,1
Hexafluoroetano	173,08	26,60
Hidrogênio	13,84	7,04
Cloreto de Hidrogênio	158,96	13,9
Iodo^[7]	386,65	12,07
Isobutano^[8]	113,55	1,9481 × 10⁻⁵
Mercúrio	234,2	1,65 × 10⁻⁷
Metano	90,68	11,7
Neon	24,57	43,2
Óxido nítrico	109,50	21,92
Nitrogênio	63,18	12,6
Óxido nitroso	182,34	87,85
Oxigênio	54,36	0,152
Paládio	1825	3,5 × 10⁻³
Platina	2045	2,0 × 10⁻⁴
Dióxido de enxofre	197,69	1,67
Titânio	1941	5,3 × 10⁻³
Hexafluoreto de urânio	337,17	151,7
Água	273,16	0,6117
Xenônio	161,3	81,5
Zinco	692,65	0,065

/ G ψ = E ψ =

\psi ^{*}

E [tG+].... ../ c

Pesquisar este blog

MECÂNICA GENERALIZADA GRACELI - QUÂNTICA QUÍMICA RELATIVISTA [106]

Força fundamental - INTERAÇÕES GRACELI IG =

IGFF = INTERAÇÕES GRACELI - Força fundamental.

T = TEMPERATURA.

IGFF = FF / T . PM. ISO . MM. DEEQ. NE. BE. [1]

1 / IGFF = FF / T . PM. ISO . MM. DEEQ. NE. BE. [-1]

IGFF = FF / T . PM. ISO . MM. DEEQ. NE. BE. / c .

Explicação

História

Classes cristalinas piroelétricas

Desenvolvimentos recentes

Descrição matemática

Mecanismo

Cristais

Descrição matemática

Substâncias puras: ponto crítico líquido-vapor

Definição matemática

Células do ponto triplo

Tabela de pontos triplos

Comentários

Postar um comentário